Type systems

Let \( T \) be a set of all possible values which may appear in our language of expressions. For example, 1, "Hello world", '(1 2 3) all may belong to \( T \). A type as type-inference-engine understands it is a subset of \( T \). A type system \( I \) is a set of all types. \( I \) is a partially ordered set: it is said that for \(t_1, t_2 \in I \), \(t_1 \le t_2 \) if \( t_1 \subset t_2 \) and \( t_1 = t_2 \) if \( t_1 \subset t_2 \) and \( t_2 \subset t_1 \). \( I \) is also a lattice: for each \( t_1, t_2 \in I \) there are unique meet \( t_1 \wedge t_2 \in I\) and join \(t_1 \vee t_2 \in I \).

Join is defined as the smallest type such as \( t_1 \subset t_1 \vee t_2 \) and \( t_2 \subset t_1 \vee t_2 \) and meet is the biggest type such as \( t_1 \wedge t_2 \subset t_1 \) and \( t_1 \wedge t_2 \subset t_2 \). To form a lattice from a set of disjoint types, we include a type \( T \)(all possible values) and a type \( \emptyset \)(no values belong to this type) in our type system. So if \(t_1 \cap t_2 = \emptyset \), then \(t_1 \vee t_2 = T \) and \(t_1 \wedge t_2 = \emptyset \).

The type system \( I \) can be represented as a directed graph. For example, in the example package type-inference-engine/example it is defined as follows: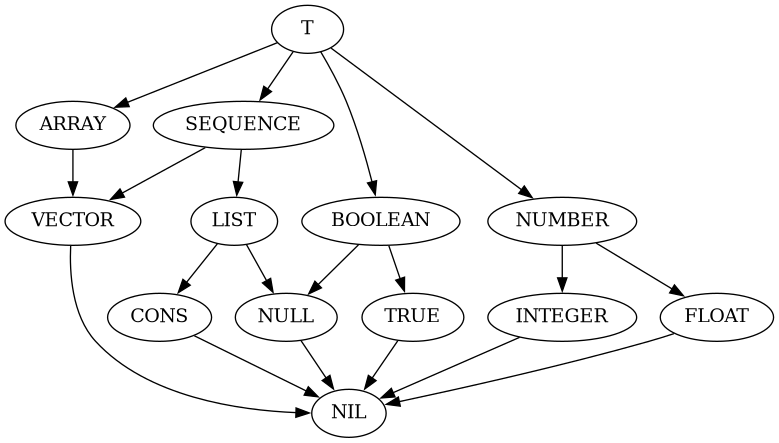

Here a connection from ARRAY to VECTOR means that VECTOR ⊂ ARRAY. A description of types follows:

T is a type \(T\) which contains all possible values in the program.
ARRAY is a type for arrays of any dimensionality, e.g. #(1 2 3), #2a((1 2 3)(1 2 3)).
SEQUENCE is a type for collections which can be indexed by a non-negative integer, e.g. #(1 2 3), '(1 2 3).
VECTOR is a type for one-dimensional arrays, e.g. #(1 2 3).
LIST is a type for lists. List is either a cons cell or a value NIL. Examples: NIL, '(1 2 3), '(1 2 . 3).
BOOLEAN is a type which contains two values: NIL and T.
NUMBER is a type for any number, possibly a complex number.
CONS is a type for pairs of values, or cons cells, e.g. '(1 . 4).
NULL contains only one value: NIL.
TRUE contains only one value: T.
INTEGER contains integers.
FLOAT contains floats (in any representation).
NIL is a bottom type \( \emptyset \).

NB: As a limitation of the engine, the bottom type must have a name NIL. There is no other limitations in the type naming. For example, you can name \( T \) as TOP instead of T. Here I just follow a convention used in Common Lisp.

NB: You must keep in mind the difference between a value NIL and a type NIL. The former is a value of types NULL, BOOLEAN, LIST, SEQUENCE and T and the latter is a type which has no values in it.

NB: This kind of type systems is very close to what we have in Common Lisp with exception that there is no compond types and hence no set-theoretic types like not, and and or.

Now let's define our own type system, which contains types NIL, INTEGER, REAL and T and some wrapper functions for working with that type system:

(defpackage tie-example
  (:use #:cl)
  (:local-nicknames (#:tie  #:type-inference-engine)
                    (#:sera #:serapeum))
  (:export #:*my-system*
           #:type-node-order
           #:join
           #:meet))
(in-package :tie-example)

(defparameter *my-system*
  (let* ((bottom   (tie:type-node nil "The bottom type. No value belongs to this type"
                                  ;; No subtypes
                                  nil))
         (integer  (tie:type-node 'integer "A type for integer numbers"
                                  ;; NIL is the only subtype
                                  (list bottom)))
         (real     (tie:type-node 'real "A type for real numbers"
                                  ;; INTEGERs are real numbers. INTEGER is a direct
                                  ;; subtype of REAL
                                  (list integer)))
         (string   (tie:type-node 'string "A type for strings"
                                  (list bottom)))
         (top      (tie:type-node t "The top type"
                                  ;; Two direct subtypes
                                  (list real string))))
    (tie:check-type-system top)))

(defun type-op (function)
  (lambda (type-name-1 type-name-2)
    (funcall function *my-system*
             (tie:find-type-node type-name-1 *my-system*)
             (tie:find-type-node type-name-2 *my-system*))))
             
(sera:defalias type-node-order (type-op #'tie:type-node-order))
(sera:defalias join (type-op #'tie:join))
(sera:defalias meet (type-op #'tie:meet))

Now, you can evaluate some relations between types:

CL-USER> (tie-example:type-node-order nil 'real)
:LT
CL-USER> (tie-example:type-node-order 'integer 'real)
:LT
CL-USER> (tie-example:type-node-order 'integer 'string)
NIL
CL-USER> (tie-example:type-node-order 'string nil)
:GT
CL-USER> (tie-example:type-node-order nil nil)
:EQ
CL-USER> (tie-example:join 'integer 'real)
#<TYPE-INFERENCE-ENGINE:TYPE-NODE REAL {100DBB6283}>
CL-USER> (tie-example:meet 'integer 'real)
#<TYPE-INFERENCE-ENGINE:TYPE-NODE INTEGER {100DBB6263}>
CL-USER> (tie-example:join 'integer 'string)
#<TYPE-INFERENCE-ENGINE:TYPE-NODE T {100DBB62C3}>
CL-USER> (tie-example:meet 'integer 'string)
#<TYPE-INFERENCE-ENGINE:TYPE-NODE NIL {100DBB6243}>