neural-classifier

Optimizers

By default, neural-classifier:train-epoch uses stochastic gradient descent (SGD) algorithm to minimize the cost function. There are other optimizers which can be used during learning. You can create an optimizer by instantiating of of the optimizer classes (which are subclasses of neural-classifier:optimizer) and pass it to neural-classifier:train-epoch function. A complete list of optimizers is below. A symbol \(f\) present in the documentation denotes the cost function. A learning rate is specified using :η initarg. Initargs :β1 and :β2 are common for optimizers with momentum and variable learning rate respectively.

optimizer
Superclasses(t)
Metaclassstandard-class
Default Initargsnil
Generic optimizer class. Not to be instantiated
  • learning-rate
    Parameter which controls learning speed of the neural network. Must be a small positive value.
    Allocationinstance
    Typesingle-float
    Initarg:η
    Readers(optimizer-learning-rate)
  • minibatch-size
    Number of samples in a minibatch. An integer in the range 10-100 is good for this parameter.
    Allocationinstance
    Typealexandria:positive-fixnum
    Initarg:minibatch-size
    Initform40
    Readers(optimizer-minibatch-size)
  • decay-rate
    A parameter used for L² regularization. 0.0 is no regularization. Good values are 1-10 divided by the dataset size.
    Allocationinstance
    Typesingle-float
    Initarg:decay-rate
    Initform0.0
    Readers(optimizer-decay-rate)
sgd-optimizer
Superclasses(optimizer t)
Metaclassstandard-class
Default Initargs(:η 0.01)
A basic stochastic gradient optimizer. A parameter \(w\) of a neural network is updated as \(w_{n+1} = w_n - \eta \nabla f(w_n)\).
    momentum-optimizer
    Superclasses(momentum-memo-optimizer t)
    Metaclassstandard-class
    Default Initargs(:η 0.01 :β1 0.9)

    Stochastic gradient descent optimizer with momentum. A parameter \(w\) of a neural network is updated with respect to an accumulated momentum \(m\):

    \(m_{n+1} = \beta_1 m_{n} + \eta \nabla f(w_n)\)

    \(w_{n+1} = w_n - m_{n+1}\)

      nesterov-optimizer
      Superclasses(momentum-memo-optimizer t)
      Metaclassstandard-class
      Default Initargs(:η 0.01 :β1 0.9)

      Nesterov optimizer: a stochastic gradient descent with momentum and 'look-ahead'. A parameter \(w\) of a neural network is updated with respect to an accumulated momentum \(m\):

      \(m_{n+1} = \beta_1 m_{n} + \eta \nabla f(w_n - \beta_1 m_n)\)

      \(w_{n+1} = w_n - m_{n+1}\)

        adagrad-optimizer
        Superclasses(rate-memo-optimizer t)
        Metaclassstandard-class
        Default Initargs(:η 0.01)

        Adagrad optimizer: an optimizer with decaying learning rate. A parameter \(w\) of a neural network is updated as follows:

        \(s_{n+1} = s_n + (\nabla f(w_n))^2\)

        \(w_{n+1} = w_n - \frac{\eta}{\sqrt{s_{n+1} + \epsilon}} \nabla f(w_n)\)

          rmsprop-optimizer
          Superclasses(rate-memo-optimizer t)
          Metaclassstandard-class
          Default Initargs(:η 0.001 :β2 0.99)

          RMSprop optimizer: an optimizer with adaptive learning rate. A parameter \(w\) of a neural network is updated as follows:

          \(s_{n+1} = \beta_2 s_n + (1 - \beta_2)(\nabla f(w_n))^2\)

          \(w_{n+1} = w_n - \frac{\eta}{\sqrt{s_{n+1} + \epsilon}} \nabla f(w_n)\)

            adam-optimizer
            Superclasses(momentum-memo-optimizer rate-memo-optimizer t)
            Metaclassstandard-class
            Default Initargs(:η 0.001 :β1 0.9 :β2 0.999)

            ADAM optimizer: an optimizer with adaptive learning rate and momentum. A parameter \(w\) of a neural network is updated as follows:

            \(m_{n+1} = \beta_1 m_n + (1 - \beta_1) \nabla f(w_n)\)

            \(s_{n+1} = \beta_2 s_n + (1 - \beta_2)(\nabla f(w_n))^2\)

            \(\hat{m} = m_{n+1} / (1 - \beta_1^n) \)

            \(\hat{s} = s_{n+1} / (1 - \beta_2^n) \)

            \(w_{n+1} = w_n - \frac{\eta}{\sqrt{\hat{s} + \epsilon}} \hat{m}\)

            • corrected-momentum-coeff
              Corrected \(\beta_1\) parameter
              Allocationinstance
              Typesingle-float
              Initform1.0
              Accessors(optimizer-corrected-momentum-coeff)
            • corrected-rate-coeff
              Corrected \(\beta_2\) parameter
              Allocationinstance
              Typesingle-float
              Initform1.0
              Accessors(optimizer-corrected-rate-coeff)

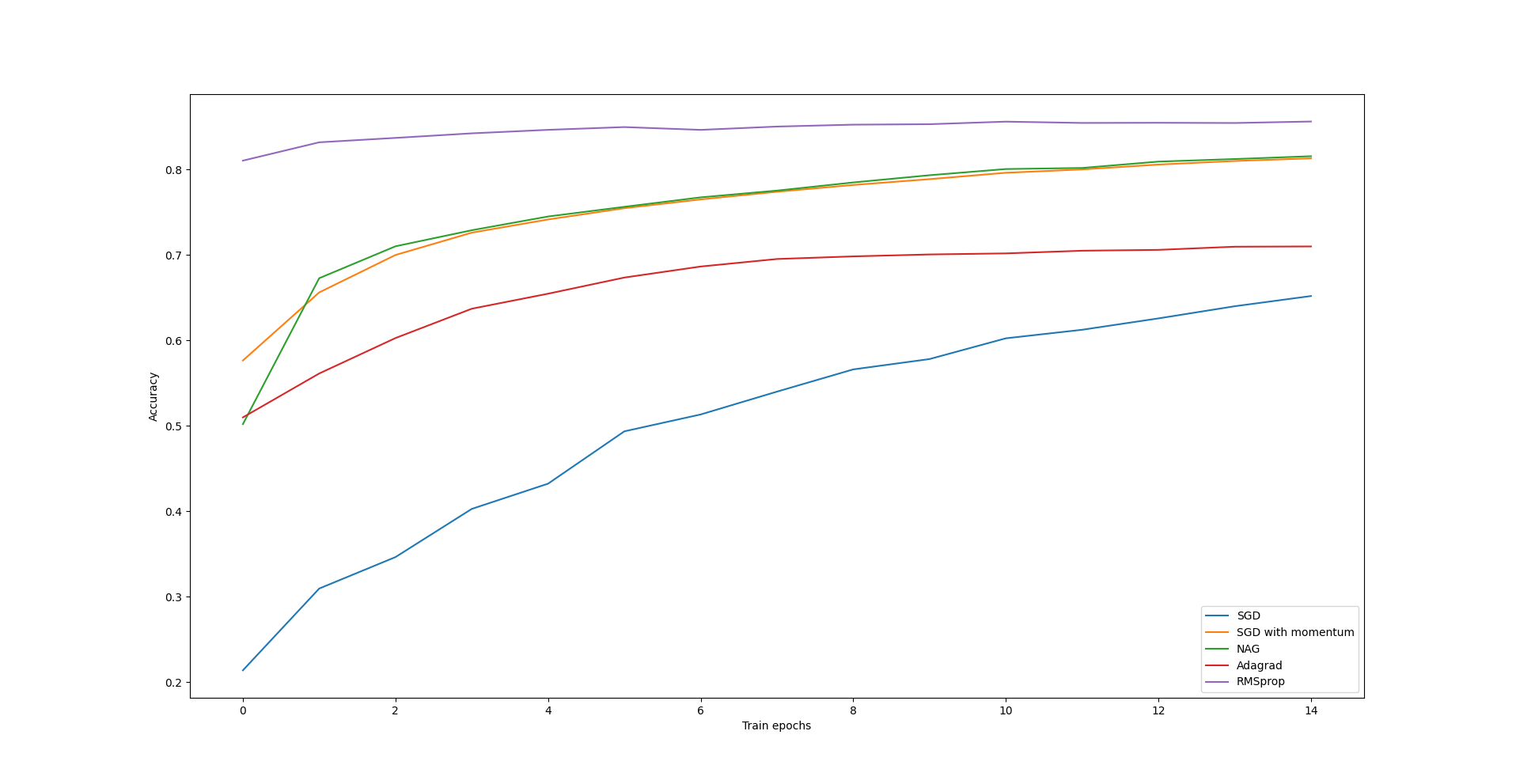
            Here is a plot showing how accuracy of classification of test data from fashion MNIST set varies with the number of training epochs. Networks used in this example have one hidden layer with 50 neurons. All activation functions are sigmoids. Accuracy are averaged from 3 independent runs.